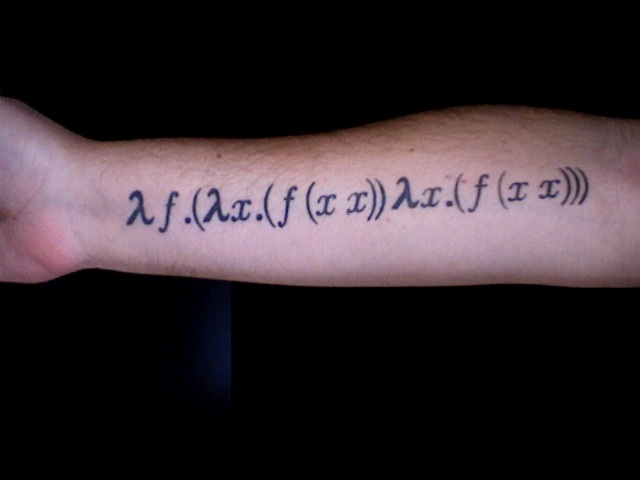Compiling to lambda-calculus: Turtles all the way down

[article index] [] [@mattmight] [rss]

My compilers class always starts with a full lecture on the lambda-calculus.

It leaves behind only the dedicated.


Barendregt is a helluva drug.

The lambda-calculus is a minimal programming language.

Though it contains forms only for function applications, variable references and anonymous functions, it is equivalent to a Turing machine.

That equivalence is not obvious.

One direction of the equivalence is easy--constructing an effective method that calculates the value of an expression in the lambda-calculus.

(We know how to implement effective methods as Turing machines.)

The other direction requires more thought: how do you coax such a simple language into providing the features we expect of a modern programming language, such as numbers, Booleans, conditionals, lists and recursion?

(Once you've got these features, it's easy to simulate a Turing machine.)

To illustrate how it's done, this article contains a working compiler written in Racket that translates a small, clearly-universal functional programming language into the pure lambda-calculus.

These techniques are useful when constructing a compiler: once anonymous functions work, you can implement unfinished features with desugarings.

Read on for explanations, examples and code.

[Update: The owner of the tattooed arm has stepped forward: Turing Eret!]

The λ-calculus

The λ-calculus is a language with three expression forms:

  • variable reference, e.g., v, foo;
  • function application, e.g., (f x), (f (g x)); and
  • anonymous functions, e.g., (λ (v) (+ v 1)).
Or, in BNF: 
      <exp> ::= <var>
             |  (<exp> <exp>)
             |  (λ (<var>) <exp>)

Don't be fooled by its size: this language is Turing-complete.

The λ-calculus is the assembly language of mathematics.

A small language

The language from which we'll compile into the λ-calculus is a small functional language, a clearly-Turing-complete subset of Scheme: 

 <exp> ::= <var>

        |  #t
        |  #f
        |  (if  <exp> <exp> <exp>)
        |  (and <exp> <exp>)
        |  (or  <exp> <exp>)

        |  <nat>
        |  (zero? <exp>)
        |  (- <exp> <exp>)
        |  (= <exp> <exp>)
        |  (+ <exp> <exp>)
        |  (* <exp> <exp>)

        |  <lam>
        |  (let ((<var> <exp>) ...) <exp>)
        |  (letrec ((<var> <lam>)) <exp>)

        |  (cons <exp> <exp>)
        |  (car  <exp>)
        |  (cdr  <exp>)
        |  (pair? <exp>)
        |  (null? <exp>)
        |  '()

        |  (<exp> <exp> ...)

 <lam> ::= (λ (<var> ...) <exp>)

We'll use Church encodings to provide the atomic and compound data structures for our small language.

A Church encoding is a way of representing a value such as a number, a Boolean or a list as a procedure.

The compile function

The compile function drives the translation by matching and dispatching on the form of the expression; code for individual cases are provided below: 

; Compilation:
(define (compile exp)
  (match exp
    
    ; Symbols stay the same:
    [(? symbol?)         exp]
    
    ; Boolean and conditionals:
    [#t                  ...]
    [#f                  ...]
    [`(if ,cond ,t ,f)   ...]
    [`(and ,a ,b)        ...]
    [`(or ,a ,b)         ...]

    ; Numerals:
    [(? integer?)        ...]
    [`(zero? ,exp)       ...]
    [`(- ,x ,y)          ...]
    [`(+ ,x ,y)          ...]
    [`(* ,x ,y)          ...]
    [`(= ,x ,y)          ...]
 
    ; Lists:
    [ (quote '())        ...]
    [`(cons  ,car ,cdr)  ...]
    [`(car   ,list)      ...]
    [`(cdr   ,list)      ...]
    [`(pair? ,list)      ...]
    [`(null? ,list)      ...]
    
    ; Lambdas:
    [`(λ () ,exp)           ...]
    [`(λ (,v) ,exp)         ...]
    [`(λ (,v ,vs ...) ,exp) ...]

    ; Binding forms:
    [`(let ((,v ,exp) ...) ,body)  ...]
    [`(letrec [(,f ,lam)] ,body)   ...]
    
    ; Application -- must be last:
    [`(,f)                    ...]
    [`(,f ,exp)               ...]
    [`(,f ,exp ,rest ...)     ...]
    
    [else  
     (display (format "unknown exp: ~s~n" exp))
     (error "unknown expression")]))

This skeleton highlights a coding pattern that appears throughout the construction of compilers and interpreters.

Multi-argument functions

Multi-arguments functions are reduced to single-argument functions. Instead of accepting multiple arguments, a procedure accepts the first argument and returns a procedure that accepts the remainder.

Specifically, a multi-argument lambda term: 

 (λ (v1 ... vN) body)

turns into: 

 (λ (v1) 
  (λ (v2)
   ...
    (λ (vN)
     body)))

while an application form with multiple arguments: 

 (f arg1 ... argN)

becomes: 

 (... ((f arg1) arg2) ... argN)

The following cases in the function compile transform λ-terms: 

    ; Lambdas:
    [`(λ () ,exp)           
     ; =>
     `(λ (_)  ,(compile exp))] 
    
    [`(λ (,v) ,exp)         
     ; =>
     `(λ (,v) ,(compile exp))]
    
    [`(λ (,v ,vs ...) ,exp)
     ; =>
     `(λ (,v)
        ,(compile `(λ (,@vs) ,exp)))]

while the following cases at the end handle applications: 

    ; Application -- must be last:
    [`(,f) 
     ; =>
     (compile `(,(compile f) ,VOID))]
    
    [`(,f ,exp)
     ; =>
     `(,(compile f) ,(compile exp))]
    
    [`(,f ,exp ,rest ...)
     ; =>
     (compile `((,f ,exp) ,@rest))]
    
    [else  
     ; =>
     (display (format "unknown exp: ~s~n" exp))
     (error "unknown expression")]))

This technique is called Currying.

VOID is a dummy function that we never expect to invoke: 

; Void.
(define VOID  `(λ (void) void))

Booleans and conditionals

The core trick to Church encodings is to encode a data value in the form of the computation that uses it.

Consider Booleans: true and false.

How are true and false used?

They appear as the condition in an if form.

A Boolean performs branching between two potential computations.

So, a Boolean takes in two computations (encoded as functions) and executes one of them.

The encoding for true will execute the "true" computation; the encoding for false will execute the "false" computation: 

; Booleans.
(define TRUE  `(λ (t) (λ (f) (t ,VOID))))
(define FALSE `(λ (t) (λ (f) (f ,VOID))))

The cases for compile turn the condition into the procedure: 

    ; Boolean and conditionals:
    [#t              TRUE]
    [#f              FALSE]
 
    [`(if ,cond ,t ,f)
     ; =>
     (compile `(,cond (λ () ,t) (λ () ,f)))]

    [`(and ,a ,b)
     ; =>
     (compile `(if ,a ,b #f))]
    
    [`(or ,a ,b)
     ; =>
     (compile `(if ,a #t ,b))]

Church numerals

There are many different ways to encode numbers as computation.

Consider the ways in which numbers are used: counting, measuring, indexing, ordering and iterating.

Iterating turns out to be a general way of encoding numbers.

That is, we can encode the number n as a function that invokes another function n times.

The procedure church-numeral takes a natural number and yields the code for a procedure f with the signature:

f : (α -> α) -> α > α

so that:

f(g)(z) = gn(z)

The code for church-numeral is short: 

; Church numerals.
(define (church-numeral n)
  
  (define (apply-n f n z)
    (cond
      [(= n 0)  z]
      [else     `(,f ,(apply-n f (- n 1) z))]))
       
  (cond
    [(= n 0)    `(λ (f) (λ (z) z))]
    [else       `(λ (f) (λ (z) 
                          ,(apply-n 'f n 'z)))]))

Under this iterative representation, we can encode addition, subtraction, multiplication and equality comparison: 

(define ZERO? `(λ (n)
                 ((n (λ (_) ,FALSE)) ,TRUE)))
                  
(define SUM '(λ (n)
               (λ (m)
                 (λ (f)
                   (λ (z)
                     ((m f) ((n f) z)))))))

(define MUL '(λ (n)
               (λ (m)
                 (λ (f)
                   (λ (z)
                     ((m (n f)) z))))))
                     
(define PRED '(λ (n)
                (λ (f)
                  (λ (z)
                    (((n (λ (g) (λ (h) 
                                  (h (g f)))))
                      (λ (u) z))
                     (λ (u) u))))))

(define SUB `(λ (n)
               (λ (m)
                 ((m ,PRED) n))))

so that the cases for compile drop in the right definitions: 

    ; Numerals:
    [(? integer?)     (church-numeral exp)]
    [`(zero? ,exp)   `(,ZERO? ,(compile exp))]
    [`(- ,x ,y)      `((,SUB ,(compile x)) ,(compile y))]
    [`(+ ,x ,y)      `((,SUM ,(compile x)) ,(compile y))]
    [`(* ,x ,y)      `((,MUL ,(compile x)) ,(compile y))]
    [`(= ,x ,y)       (compile `(and (zero? (- ,x ,y))
                                     (zero? (- ,y ,x))))]

Representing lists

A list is an object with one operation: destructuring match.

A match on a list takes two operands: a function to invoke with the head of the list and the rest, and a function to invoke if the list is empty.

A Church-encoded list is then a function that takes two operands--a function to invoke with the head of the list and the rest, and a function to invoke if the list is empty: 

; Lists.
(define CONS `(λ (car) 
                (λ (cdr)
                  (λ (on-cons)
                    (λ (on-nil)
                      ((on-cons car) cdr))))))

(define NIL `(λ (on-cons)
               (λ (on-nil)
                 (on-nil ,VOID))))

(define CAR `(λ (list)
               ((list (λ (car)
                       (λ (cdr)
                         car)))
                ,ERROR)))

(define CDR `(λ (list)
               ((list (λ (car)
                       (λ (cdr)
                         cdr)))
                ,ERROR)))

(define PAIR? `(λ (list)
                 ((list (λ (_) (λ (_) ,TRUE)))
                  (λ (_) ,FALSE))))

(define NULL? `(λ (list)
                 ((list (λ (_) (λ (_) ,FALSE)))
                  (λ (_) ,TRUE))))

so that the cases in compile merely drop these in: 

    ; Lists:
    [ (quote '())         NIL]
    [`(cons  ,car ,cdr)  `((,CONS ,(compile car)) 
                           ,(compile cdr))]
    [`(car   ,list)      `(,CAR   ,(compile list))]
    [`(cdr   ,list)      `(,CDR   ,(compile list))]
    [`(pair? ,list)      `(,PAIR? ,(compile list))]
    [`(null? ,list)      `(,NULL? ,(compile list))]

Desugaring let

A let form turns into the immediate application of a λ-term.

Specifically, the form: 

 (let ((v1 exp1) ... (vN expN)) body)

becomes: 

 ((λ (v1 ... vN) body) exp1 ... expN)

A single case in compile handles let forms: 

    ; Binding forms:
    [`(let ((,v ,exp) ...) ,body)
     ; =>
     (compile `((λ (,@v) ,body) ,@exp))]

Recursion: The Y combinator

To handle recursion, we'll invoke the Y combinator. (I've explained the Y combinator and fixed points in another post.)

The Y combinator computes a recursive function as the fixed point of a non-recursive function.

Remarkably, the Y combinator may be expressed directly in the λ-calculus: 

; Recursion.
(define Y '((λ (y) (λ (F) (F (λ (x) (((y y) F) x))))) 
            (λ (y) (λ (F) (F (λ (x) (((y y) F) x)))))))

which allows the compile procedure to handle letrec with a single case: 

    [`(letrec [(,f ,lam)] ,body)
     ; =>
     (compile `(let ((,f (,Y (λ (,f) ,lam))))
                 ,body))]

The FFI: Unchurchifiers

It's not particularly useful to compile to a target language unless there's a way of interacting with that target language.

To convert procedural encodings of numbers, Booleans and lists back into Racket values, we need unchurchifiers: 

; Unchurchification.
(define (succ n) (+ n 1))

(define (natify church-numeral)
  ((church-numeral succ) 0))

(define (boolify church-boolean)
  ((church-boolean (λ (_) #t)) (λ (_) #f)))

(define (listify f church-list)
  ((church-list
    (λ (car) (λ (cdr) (cons (f car) (listify f cdr)))))
   (λ (_) '())))

The functions natify, boolify and listify perform the deconversion.

Example: Factorial

Consider a program, R1, which computes factorial: 

(define R1 (compile `(letrec [(f (λ (n) 
                                   (if (= n 0)
                                       1
                                       (* n (f (- n 1))))))]
                       (f 5))))

The compiled code for this program is: 

((λ (f) (f (λ (f) (λ (z) (f (f (f (f (f z)))))))))
  (((λ (y) (λ (F) (F (λ (x) (((y y) F) x)))))
    (λ (y) (λ (F) (F (λ (x) (((y y) F) x))))))
   (λ (f)
     (λ (n)
       ((((((λ (n)
              ((n (λ (_) (λ (t) (λ (f) (f (λ (void) void))))))
               (λ (t) (λ (f) (t (λ (void) void))))))
            (((λ (n)
                (λ (m)
                  ((m
                    (λ (n)
                      (λ (f)
                        (λ (z)
                          (((n (λ (g) (λ (h) (h (g f)))))
                            (λ (u) z))
                           (λ (u) u))))))
                   n)))
              n)
             (λ (f) (λ (z) z))))
           (λ (_)
             ((λ (n)
                ((n (λ (_) (λ (t) (λ (f) (f (λ (void) void))))))
                 (λ (t) (λ (f) (t (λ (void) void))))))
              (((λ (n)
                  (λ (m)
                    ((m
                      (λ (n)
                        (λ (f)
                          (λ (z)
                            (((n (λ (g) (λ (h) (h (g f)))))
                              (λ (u) z))
                             (λ (u) u))))))
                     n)))
                (λ (f) (λ (z) z)))
               n))))
          (λ (_) (λ (t) (λ (f) (f (λ (void) void))))))
         (λ (_) (λ (f) (λ (z) (f z)))))
        (λ (_)
          (((λ (n) (λ (m) (λ (f) (λ (z) ((m (n f)) z))))) n)
           (f
            (((λ (n)
                (λ (m)
                  ((m
                    (λ (n)
                      (λ (f)
                        (λ (z)
                          (((n (λ (g) (λ (h) (h (g f)))))
                            (λ (u) z))
                           (λ (u) u))))))
                   n)))
              n)
             (λ (f) (λ (z) (f z))))))))))))

And, when we eval this program and unchurchify, we get 120, as expected: 

> (natify (eval R1))
120

Code

The Racket source code is available.

More resources